
If the coefficient is negative, as the term increases, the mean value of the response decreases. The sign of the coefficient indicates the direction of the relationship between the term and the response.
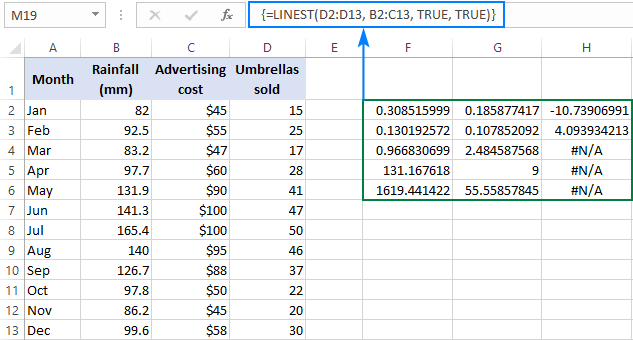
The coefficient of the term represents the change in the mean response for a one-unit change in that term. It quantifies the total variation in the data. Adj SS Total The total sum of squares is the sum of the regression sum of squares and the error sum of squares. It quantifies the variation in the data that the predictors do not explain. Adj SS Error The error sum of squares is the sum of the squared residuals. It quantifies the amount of variation in the response data that is explained by each term in the model. Adj SS Term The adjusted sum of squares for a term is the increase in the regression sum of squares compared to a model with only the other terms. It quantifies the amount of variation in the response data that is explained by the model.

Adj SS Regression The regression sum of squares is the sum of the squared deviations of the fitted response values from the mean response value. In the Analysis of Variance table, Minitab separates the sums of squares into different components that describe the variation due to different sources. The order of the predictors in the model does not affect the calculation of the adjusted sum of squares. In this example, the 95% confidence interval indicates that the engineer can be 95% confident that the mean stiffness will be between approximately 60 and 74.Īdjusted sums of squares are measures of variation for different components of the model. The prediction interval is always wider than the corresponding confidence interval. While it is unlikely that such an observation would have a stiffness of exactly 66.995, the prediction interval indicates that the engineer can be 95% confident that the actual value will be between approximately 48 and 86. The regression equation predicts that the stiffness for a new observation with a density of 25 is -21.53 + 3.541*25, or 66.995.

Then, the analyst uses the model to predict the stiffness.
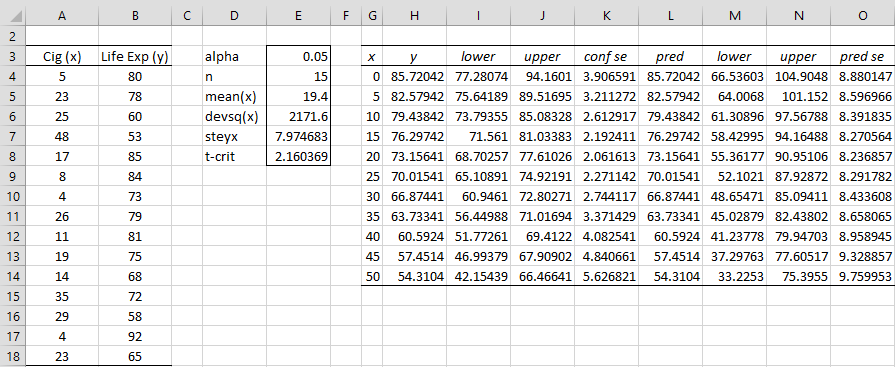
The engineer verifies that the model meets the assumptions of the analysis. (Note, however, that this is only true for density values that are within the range included in the analysis.)įor example, a materials engineer at a furniture manufacturing site develops a simple regression model to predict the stiffness of particleboard from the density of the board. With 95% prediction bands, you can be 95% confident that new observations will fall within the interval indicated by the purple lines.


 0 kommentar(er)
0 kommentar(er)
